Abstract

Deep generative models have been extensively explored in recent years, especially for the graph data such as molecules and point clouds. Yet, much less investigation has been carried out on understanding the learned latent space of deep graph generative models. Such understandings can open up a unified perspective and provide guidelines for essential tasks like controllable generation. In this paper, we first examine the representation space of the recent deep generative model trained for graph data, observing that the learned representation space is not perfectly disentangled. Based on this observation, we then propose an unsupervised method called GraphCG, which is model-agnostic plus task-agnostic for discovering steerable factors in graph data. Specifically, GraphCG learns the semantic-rich directions, via maximizing the corresponding mutual information, where the edited graph along the same direction will possess certain steerable factors. We conduct experiments on two types of graph data, molecules and point clouds. Both the quantitative and qualitative results show the effectiveness of GraphCG for discovering steerable factors. The code will be public upon acceptance.

Problem Formulation: Graph Controllable Generation

Given a pre-trained DGM (i.e., the encoder and decoder are fixed), we want to learn the most semantic-rich directions in the latent space $\mathcal{Z}$. Then for each latent vector $z$, with semantic direction $i$ and step size $\alpha$, we expect to get an edited latent vector $z_{i, \alpha}$ with an edit function $h(\cdot)$ as: $$z_{i,\alpha} = h(z, d_i, \alpha), \quad\quad \bar x' = g(z_{i,\alpha} ),$$ where $\bar x$ is the edited reconstructed data. We expect that $z_{i, \alpha}$ can inherently possess certain steerable factors, which can be reflected in $\bar x$.
The above is an example on molecular graphs editing. $z$ is the originally sampled latent representation, and $\bar z$ is the edited latent representation along a semantic vector. After decoding, from $x'$ to $\bar x'$, a steerable factor has been modified: it is a bioisostere replacement from dihydroisoxazole to dihydropyrazole (from atom O to atom N). Or to be more precise, this is a bioisostere replacement from 2,5-dihydroisoxazole to 2,3-dihydro-1H-pyrazole. Properties like LogP also change accordingly.

Method: GraphCG

Training phase: The mutual information measures the non-linear dependency between variables. And here we assume that maximizing the MI between data points with the same semantic direction and step size can maximize the shared information within each semantic direction and step size, while diversifying the semantic information among different directions or step sizes.

Test Phase: We first sample an anchor molecule, and adopt the learned directions in the training phase for editing. With step size $\alpha \in [-3, 3]$, we can generate a sequence of molecules. Specifically, in the example here, after decoding, there is a functional group change shown up: the number of hydroxyl groups decreases along the sequence in the decoded molecules.

Results: Molecular Graph Editing

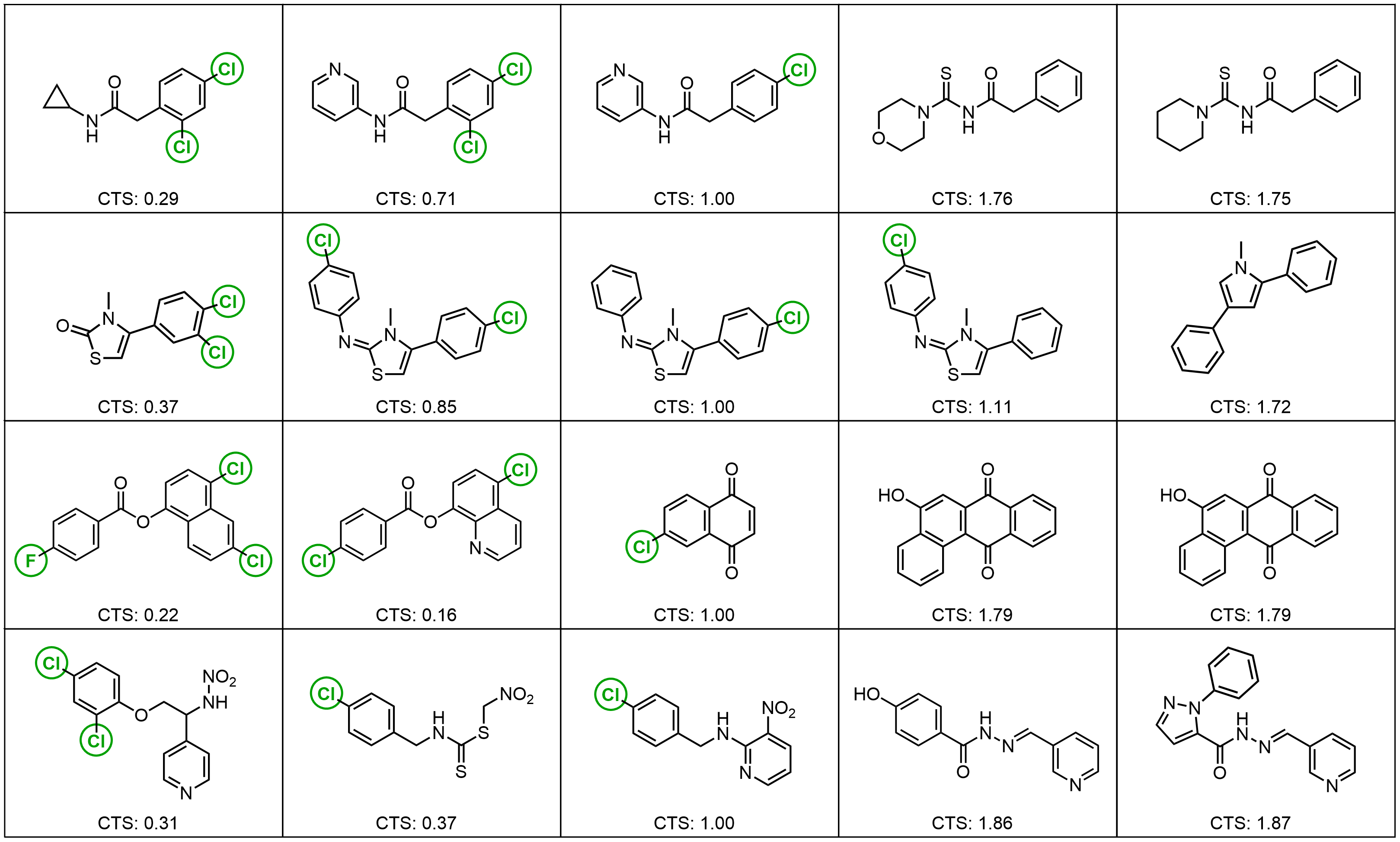
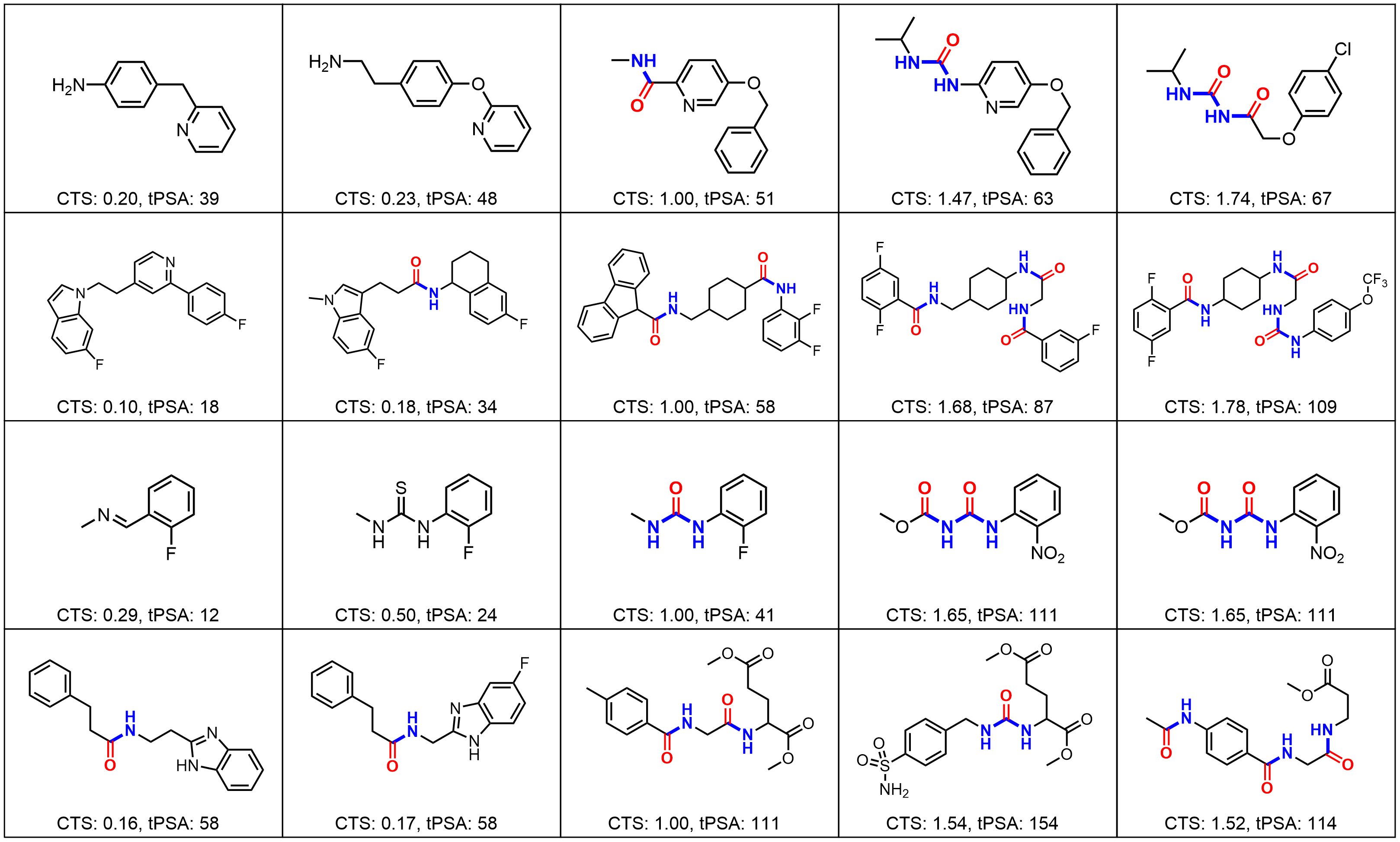
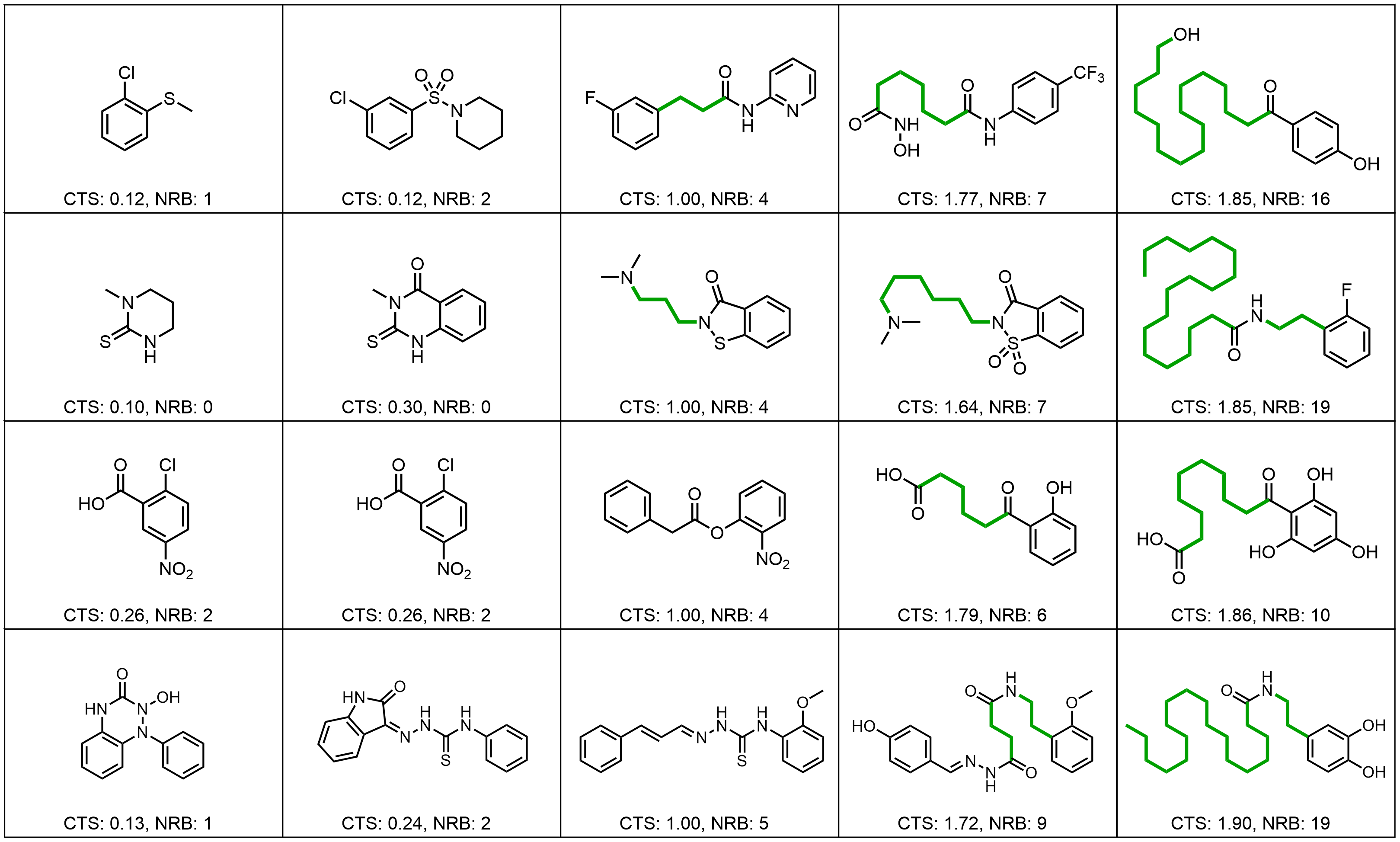
Results: Point Clouds Editing

Citation